Maxwell equations
What are the Maxwell equations?
The Maxwell equations comprise four principles and laws of electrical, magnetic, and optical phenomena. They form the most basic calculations of electrodynamics. The Maxwell equations were set up by Scottish physicist James Clerk Maxwell between 1861 and 1864. The formulas define how electrical and magnetic fields are related. In addition, Maxwell's theses also describe the relationship between electric charges and electric current under certain conditions.
The Maxwell equations today form the theoretical basis for optics, electrostatics and electrical engineering. They are a complex system of linear partial differential equations of the first order. The calculations basically describe the behavior of electromagnetic waves and are therefore of great importance in physics to this day.
The four Maxwell equations and their functions
Maxwell used four formulas and their derivations for his equations, as well as various derivations that are named after him today. The physicist combined the laws known at the time into a single treatise and supplemented the equations with the displacement current. Simply explained, the physical content of Maxwell's equations can be well expressed in the well-known laws of electromagnetism:
Maxwell equation or the Coulomb law: The first equation describes that electric fields D are caused by electric charges (charge density ρ). The set of field lines of the electric field E is characterized by the divergence of a field (∇ × E).
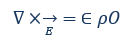
Maxwell equation: This describes that all field lines of the magnetic field B are always self-contained and there are no magnetic monopoles. The field lines do not run as a vector, but circular. In addition, the direction of the field lines is defined exactly: They always describe a circle from the north to the south pole of a magnet.
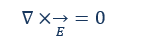
Maxwell equation: Electric fields and voltages are generated by variable magnetic fields. This is the so-called electromagnetic induction, which results from displacement currents. B stands for the magnetic flux density.
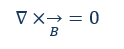
Maxwell Equation or the Law of Flooding (Ampère's Laws): This shows how magnetic fields are created by time-varying electric fields. μ0 describes the magnetic permeability of a vacuum or approximately that in the air space. j are the currents of the magnetic field.
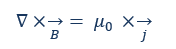
Maxwell's equations in this form always refer to the environment of a vacuum. Nevertheless, in his further considerations, he considers the matter based on material-specific parameters. This is indispensable for the description and propagation of electric and magnetic fields. The Maxwell equations have a differential and an integral form.
Why did the Maxwell equations challenge the relativity principle?
The special theory of relativity (SRT) describes the movement of fields and bodies in space and time. It was developed as an extension of the Galileo Principle of Relativity by Albert Einstein. The SRT states that all laws of physics have the same form in all inertial systems. This also applies to the field of electromagnetism, which describes the Maxwell equations.
The basic features of the SRT are that lengths and durations depend individually on the state of motion of the observer. So there is neither absolute space nor time. These assumptions are expressed in the mathematical quantity tensor. This is based on the three-dimensional space. The Maxwell equations can also be represented as stress tensor. This is called a Maxwell tensor or electromagnetic field strength sensor.
The equations are included in the special theory of relativity and describe the forces acting on a body in acceleration. At the same time, scientists have long disagreed about the absoluteness of space and time. For years, the theory of relativity could not be fully proven. Einstein then rejected these doubts with the transition from the Galileo to the Lorentz transformation. Therefore, the Maxwell equations still have a firm place in the theory of relativity.
 Thousands of products in stock
Thousands of products in stock